Otpornost Materijala

1. UVODNI POJMOVI OTPORNOSTI MATERIJALA

Na svako telo u prirodi deluju dve ili više spoljašnjih sila koje, kao što znamo iz Statike, mogu biti površinske (koje na telo deluju preko neke njegove tačke, linije ili površi) ili zapreminske (koje deluju na svaki delić tela – takva sile je, na primer, težina).

Ako na telo deluje proizvoljan sistem sila, bez obzira da li je taj sistem uravnotežen ili ne (odnosno dali telo na koje taj sistem deluje miruje ili možda ubrzava), telo se usled dejstva sila nalazi u takozvanom „napregnutom stanju“. Telo u napregnutom stanju se deformiše, što znači da mu se menjaju oblik i dimenzije.

Ako je deformacija tela zanemarljiva u odnosu na njegove dimenzije, telo nazivamo krutim. U suprotnom ga nazivamo deformabilnim. Što je sve prilično relativno. Ako, na primer, na sunđer sleti muva, nećemo ni primetiti da se sunđer pod muvinom težinom deformisao pa bi taj sunđer slobodno mogli smatrati krutim telom. Ali, ako ga stisnemo šakom, i te kako se deformiše i svakako nije krut.

Deformabilno telo na koje počinju da deluju spoljašnje sile menja svoj oblik i dimenzije, odnosno deformiše se do određene granice koja zavisi od više faktora. A o tim faktorima biće kasnije više rečeno,

U određenom trenutku dalje deformisanje se zaustavlja. Zašto? Zato što je u tom trenutku uspostavljena ravnoteža između spoljašnjih i unutrašnjih sila.

Svako materijalno telo sastoji se od molekula i atoma među kojima postoje npr. slabe privlačne sile kao kod gasova, ili veoma jake privlačne sile kao kod čvrstih tela.

Unutrašnje sile nastaju kao posledica privlačnih sila koje čestice nekog materijalnog tela drže na okupu. Pojavu unutrašnjih sila izazivaju spoljašnje sile. Deformabilno telo koje se više ne deformiše postiglo je stanje ravnoteže i možemo ga smatrati krutim. Ovo je 5. aksiom statike, odnosno 3. pretpostavka otpornosti materijala, koja nam omogućava da na napregnuto telo primenimo zakone statike. (Pretpostavke su uprošćenja koje se u neku naučnu disciplinu uvode da bi se dobili jednostavniji, a još uvek dovoljno tačni matematički modeli.)

Prva pretpostavka otpornosti materijala je pretpostavka o malim deformacijama, što znači da ćemo posmatrati isključivo napregnuta tela koja su veoma malo deformisana.

Druga pretpostavka je da svaki zamišljeni ravanski presek tela ostaje ravan i u napregnutom stanju.

2. NAPON

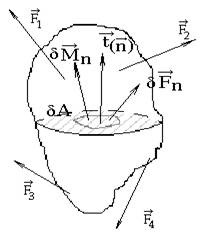
Posledica dejstva unutrašnjih sila je pojava koja se naziva napon. Napon je jedan od suštinskih pojmova otpornosti materijala. Napon je vektorska fizička veličina koja opisuje unutrašnje stanje napregnutog tela.

VRSTE NAPONA

Slika 2

Komponenta ukupnog napona (t(n)) koja ima pravac normale na površinu poprečnog preseka naziva se normalni napon (σ – sigma).

Druga komponenta ukupnog napona, koja leži u ravni preseka, naziva se tangencijalni, odnosno smičući napon (τ– tau).

3. VRSTE DEFORMACIJA

Posmatraćemo duž AB u nenapregnutom telu (slika 3), čiji ćemo pravac orijentisati vektorom (m), koji zaklapa ugao od 90° sa nekim drugim vektorom (n). Posmatramo istu duž ali u napregnutom telu (slika 4) i vidimo da je duž promenila dužinu, koja sada iznosi l, ali i položaj u odnosu na vektor (n) pa sa njim zaklapa ugao (α).

Slika 3

Veličina   naziva se apsolutno izduženje (ako je negativno onda je skraćenje), a njen količnik sa početnom dužinom je neimenovani broj

koji se naziva dilatacija ili relativno izduženje. To je prva vrsta deformacije.

Druga vrsta je klizanje, koja predstavlja razliku uglova izmedju dva posmatrana pravca u nenapregnutom i napregnutom stanju.

Slika 4.

4. AKSIJALNO NAPREZANJE

Za štap opterećen aksijalnim silama kažemo da je aksijalno napregnut. Zavisno od smera spoljašnjih sila može biti opterećen na istezanje ili na pritiskivanje

Slika 5.

Ako zamislimo da smo telo presekli po poprečnom preseku (s) i odstranili njegov desni deo, uticaj odstranjenog dela moramo zameniti unutrašnjim silama koje po preseku deluju kao površinske sile. Da bi se ostvarila ravnoteža preostalog dela štapa, rezultanta unutrašnjih sila mora biti jednaka po intezitetu spoljašnjoj sili.

Slika 6.

Pretpostavićemo da su unutrašnje sile ravnomerno raspoređene po površini poprečnog preseka i zamislićemo da je materijal štapa sačinjen od velikog broja tankih uzdužnih vlakana (ne zato što to stvarno tako izgleda, nego radi lakšeg shvatanja). U tom slučaju svako vlakno bilo bi podjednako napregnuto, a to znači da je napon u svakoj tački posmatranog poprečnog preseka isti i iznosi

4.2. DEFORMACIJE KOD AKSIJALNOG NAPREZANJA

Ako se čelični štap početne dužine   izloži zatežućoj sili (F), prvobitna dužina povećaće se za veličinu Δl, koja se naziva apsolutno izduženje, dok će ce se dimenzije poprečnog preseka smanjiti. Sa slike je jasna jednakost  . Odnos apsolutnog izduženja i početne dužine naziva se relativno izduženje ili aksijalna dilatacija.

Poprečna  dilatacija govori o promeni poprečnog preseka. Eksperimentalno je utvrdjeno da izmedju ove dve dilatacije postoji odnos   . Znak (-) je simboličkog karaktera, a označava činjenicu da se ove dve deformacije odvijaju u suprotnim smerovima (npr. ako dužina raste, poprečni presek se smanjuje). Grčkim slovom ν (ni) označen je Puasonov broj koji se nalazi u granicama izmedju 0 i 0,5 .

Za metale iznosi 0,.3< ν <0,35, to jest uzimamo približnu vrednost       

5. DIJAGRAM NAPON-DILATACIJA I HUKOV ZAKON

 Ovaj dijagram daje grafiČki prikaz zavisnosti napona i dilatacije u aksijalno napregnutom telu. Dobija se ispitivanjem ponašanja epruveta od raznih materijala na posebno konstruisanim mašinama u labaratorijskim uslovima. U prvom delu dijagram je prava linija što znači da je za te napone funkcionalna zavisnost napona i dilatacije linearna i može se izraziti funkcijom koja je poznata pod nazivom

Hukov zakon : σ = Eε .

Koeficijent proporcionalnosti u ovoj linearnoj funkciji naziva se Jungov modul elastičnosti i za čelike iznosi  .

S obzirom da je Hukov zakon matematički opis funkcionalne zavisnosti napona i dilatacije na delu dijagrama gde je ta zavisnost linearna, logično je zaključiti da taj zakon važi samo na tom delu dijagrama, do tacke P, koja se naziva granica proporcionalnosti, odnosno za napone do napona  , koji se naziva napon na granici proporcionalnosti.

Deformacije koje se javljaju u ovoj naponskoj oblasti su isključivo elastične, odnosno povratne. Takve deformacije nastaju po prestanku dejstva sile na telo, ne ostavljajući posledice. Za napone iznad tačke P, a do tačke E, (koja se naziva granica elastičnosti, a napon   napon na granici elestičnosti) deformacije su isključivo elastične. Posle tačke E počinju da se javljaju i plastične (trajne, nepovratne) deformacije, zajedno sa elastičnim. Od tacke T’, koja se naziva gornja granica tečenja, a napon koji joj odgovara napon na granici tečenja ( ili  ), dolazi do pojave da napon opada, a deformacije tela naglo rastu, kao da materijal počinje da teče. Tačka T“ naziva se donja granica tečenja, ili granica očvršćavanja, jer se posle nje dalji porast deformacija odvija uz ponovni porast napona, sve do tačke M na kojoj u materijalu počinju da se javljaju naprsline (a kojoj odgovara napon   ili  , odnosno zatezna čvrstoća), da bi uz ponovno blago padanje napona u tački S došlo do potpunog kidanje epruvete.

Hukov zakon može da se napiše u malo drugačijem obliku:

 tj.   tj 

U ovom obliku vidi se zavisnost apsolutnog izduženja od sile, početne dužine, vrste materijala i veličine poprečnog preseka. Proizvod u imeniocu (EA) često se naziva „krutost pri istezanju“.

6. DIMENZIONISANJE

Pod dimenzionisanjem se podrazumeva računski postupak odredjivanja dimenzija koje posmatrano telo treba da ima da bi izdržalo opterećenje kojem je izloženo. Pod dimenzionisanjem se takodje podrazumeva i odredjivanje intenziteta opterećenja koje telo datih dimenzija može da izdrži (odredjivanje nosivisti). Bilo da odredjujemo potrebne dimenzije na osnovu opterećenja, bilo da odredjujemo dozvoljeno opterećenje na osnovu dimenzija, to činimo sa namerom da sprečimo pojavu trajnih deformacija ili loma.

Da bi to bilo ostvareno, napon u telu mora biti manji ili u najgorem slučaju jednak dozvoljenom naponu. Matematički izraz ove tvrdnje   nazivaćemo osnovnim uslovom dimenzionisanja. Dozvoljeni napon je najveći napon koji se može dozvoliti u elementu konstrukcije, a da taj element ne izgubi svoju funkcionalnost. Za dozvoljeni napon uzimamo napon koji je nekoliko puta manji od opasnog napona. Kao opasni napon uzima se granica tečenja  , uglavnom kod žilavih materijala, kao što su čelici. Kod krtih materijala (liveno gvoždje) lom je verovatniji pa se kao opasni napon uzima zatezna čvrstoća  . Da bi se uzele u obzir moguće nepravilnosti u strukturi ili sastavu materijala od kojeg je element konstrukcije napravljen, kao i moguća odstupanja od predvidjenog načina korišćenja konstrukcije, ali i nesavršenost procesa konstruisanja, opasni napon delimo stepenom sigurnosti (S), pa je:

 ili 

ZADACI – AKSIJALNO NAPREZANJE

1.1 Odrediti prečnik štapa kružnog poprečnog preseka opterećenog na istezanje silom F=100kN, ako je dozvoljeni napon σd= 8•107 N/m2

(R: d=39,9mm usvajamo d=40mm)

Varijante za vežbu: 1. F=120 kN, σd=107 N/m2

2. F=80 kN, σd=8•106 N/m2

1.2 Štap kvadratnog poprečnog preseka opterećen je na pritiskivanje silom F= 80kN. Odrediti stranicu a poprečnog preseka, ako je dozvoljeni napon σd= 6•107 N/m2

(R: a=36,5mm usvaja se a=37mm)

Varijante za vežbu: 1. F=100 kN, σd=2•107 N/m2

2. F=120 kN, σd=4•107 N/m2

1.3 Odrediti unutrašnji prečnik cevi kružnog poprečnog preseka opterećene aksijalnom silom F=80kN, ako je dozvoljeni napon σd= 6•107 N/m2, a spoljašnji prečnik (ds) je 12cm.

(R: du=112,7mm usvaja se du=112)

Varijante za vežbu: 1. F=100 kN, ds=1,5 dm . 2. F=120 kN, ds=0,2 m

1.4 Cev kvadratnog poprečnog preseka opterećena je aksijalnom silom F= 100kN. Odrediti spoljašnju stranicu poprečnog preseka (a), ako je unutrašnja stranica (b) 6cm, a dozvoljeni napon σd= 8•107 N/m2

(R: a=69,64mm usvaja se a=70mm)

1.5 Dimenzionisati aksijalno napregnutu cev od materijala čiji je dozvoljeni napon σd= 8•107 N/m2, ako je:

a) cev kružnog poprečnog preseka, sila iznosi 100kN, a spoljašnji prečnik je za 10% veći od unutrašnjeg

Varijante za vežbu: 1. F=120 kN 2. F=80 kN

b) cev kvadratnog poprečnog preseka, sila iznosi 200kN, a unutrašnja stranica poprečnog preseka je za 10% manja od spoljašnje

Varijante za vežbu: 1. F=180 kN 2. F=210 kN

(a R: du=87,1 mm, usvaja se du=87mm, ds=95,81mm, usvaja se ds=96mm)

(b R: a=114,7mm, usvaja se a=115mm, b=103,23mm, usvaja se b=104mm)

1.6 Štap dužine lo=2m, pravougaonog poprečnog preseka, stranica a=0,1m i b=0,05m, izduži se pod dejstvom neke aksijalne sile za ∆l=0,0003m. Izračunati skraćenje stranica a i b, ako je Puasonov broj ν=1/3, i silu ako je modul elastičnosti E=2•1011N/m2.

(R: ∆a=-5•10-6m, ∆b=-2,5•10-6m, F=150kN)

1.7 Štap kvadratnog poprečnog preseka stranice a=0,1m, izduži se pod dejstvom sile F=100kN na dužinu l=2,2m. Izračunati početnu dužinu štapa ako je E=2•1011 N/m2

(R: lo=2,19989m)

1.8 Cev kružnog poprečnog preseka zategnuta je silom F=150kN. Dimenzionisati cev tako da debljina zida (δ) bude 1cm, ako je σd= 8•107 N/m2.

(R: du=49,68mm, usvaja se du=50mm, ds=70mm)

1.9 Dimenzionisati štap AB, kvadratnog poprečnog preseka, za čiji kraj A je pričvršćena kugla težine 80kN, ako je kugla oslonjena još i na kosu ravan. σd= 6•107 N/m2.

(R: a=25,82mm usvaja se a=26 mm)

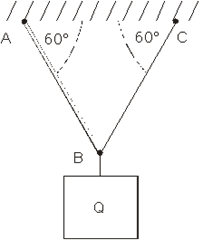
1.10 Teret težine Q=100kN okačen je na štap AB i uže BC kao na slici. Dimenzionisati štap AB, ako je σd=8•107 N/m2. Štap je kružnog poprečnog preseka.

 (R: d=30,3mm, usvaja se d=31mm)

Varijante za vežbu: 1. 

2. 

1.11 Kugla težine 60kN može biti okačena na dva predložena načina (a i b).

Odrediti potreban prečnik štapa AB, kružnog poprečnog preseka, za oba slučaja, ako je

dozvoljeni napon materijala štapa σd= 12•107 N/m2.

(a R: d=25,2m usvaja se d=26mm)

(b R: d=0,0271m usvaja se d=27mm)

1.12. Gredu težine Q=30kN, dužine l=2m pridržava čelično uže sastavljeno od n=24 žice, koje sa nepokretnom ravni zaklapa ugao od 60 stepeni.

Odrediti potreban prečnik žice ako je dozvoljeni napon σd = 8 ∙ 107 N/m2 .

( R : d ≥ 3,9 mm, usvaja se d = 4 mm ).

Varijante za vežbu: 1. Q=10000N, α=75°, n=10

2. Q=25 kN, α=15°, n=12

1.13 Teret Q okačen je kao na slici. Štap AC je čelični, prečnik mu je d1 = 30 mm, a σd1 = 16x 107 N/m2. Štap BC je od aluminijuma, d2 = 40 mm, a σd2 = 6 ∙ 107 N/m2. Koliki teret može da izdrži ova konstrukcija?

( R : Q ≤ 130,53 kN ).

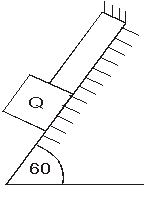
1.14 Kugla težine Q = 60 kN oslonjena na glatku ravan nagiba 60° i na njoj paralelan drveni podupirač kvadratnog poprečnog preseka stranice a = 300 mm. Ako je dozvoljeni napon za materijal podupirača σd = 3  ∙ 104 N/m2, proveriti da li je napon u podupiraču u dozvoljenim granicama.

( R : σ = 0,33  ∙ 106 N/m2 > σd => NIJE. Stranica podupirača treba da bude a ≥ 1m )

1.15 Radni pritisak u cilindru parne masine p = 106 N/m2, a prečnik cilindra je D = 350 mm. Sa koliko zavrtnja prečnika d = 18 mm treba pričvrstiti poklopac cilindra ako je dozvoljeni napon za materijal zavrtnja σd = 4 kN/cm2 .

( R : n ≥ 9,45, usvaja se n = 10 ).

Varijante za vežbu:

1. p=2000 kN/m2, D=30 cm d=0,18cm, σd =4 ∙ 104 N/mm2

2. p=400 N/cm2, D=2,8 dm d=2 cm, σd =4 ∙ 104 daN/dm2

1.16 Telo težine Q = 50 kN nalazi se na hrapavoj ravni nagibnog ugla α=60° i koeficijenta trenja µ = 0,5 . U stanju mirovanja održava ga uže sastavljeno od n=20 žica. Odrediti prečnik žice ako je dozvoljeni napon za materijal žice

σd = 6 ∙ 108 N/m2 .

( R : d ≥ 1,8 mm, usvaja se d = 2 ).

Varijante za vežbu: 1. α=30°, µ = 0,25, n=10 2. α=45°, µ = 0,3, n=12

1.17 a) Odrediti potrebne dimenzije poprečnog preseka štapova opterećenih kao na slici, ako je dozvoljeni napon pri zatezanju σdZ = 6 ∙ 106 N/m2 a pri pritiskivanju σdP = 4 ∙ 106 N/m2. . Štap 1 je kružnog, a štap 2 kvadratnog poprečnog preseka (varijanta A ), a u varijanti B štap 1 je kvadratnog, a 2 kružnog poprečnog preseka.

b) Ako je dužina štapa 1  l0 = 4 m, Jungov modul elastičnosti E = 2 ∙ 1011 N/m2 , Puasonov broj

ν=1/3 , izračunati izduženje (skraćenje) štapa Δl, kao i promenu dimenzije poprečnog preseka (Δd za varijantu A, Δa za varijantu B).

Vrednosti uglova date su u tablici.

8. STATIČKI NEODREDJENI ZADACI

Ako je broj reakcija veza veći od broja jednačina dobijenih na osnovu statičkih uslova ravnoteže zadatak je statički neodredjen. Medjutim, ukoliko možemo da formiramo dodatne jednačine, npr. na osnovu odnosa deformacija delova konstrukcije, zadatak se može rešiti.

Primer a: Štap je uklješten na oba kraja i aksijalno opterećen. Imamo dve nepoznate – sile u uklještenjima, koje ne možemo izračunati iz samo jednog uslova ravnoteže, tj. da je zbir svih aksijalnih sila jednak nuli. Dodatnu jednačinu možemo formirati iz sledeće činjenice – štap se ne može ni izdužiti, ni skratiti, jer je uklješten na oba kraja. Prema tome, koliko se jedan deo štapa (levi u ovom slučaju) izduži, toliko se drugi deo mora skratiti.

Reakcije veze smo odredili da bi smo mogli da izračunamo napone u levom i desnom delu štapa.

Kada smo izračunali napone, možemo pristupiti dimenzionisanju štapa i to na sledeći način: utvrdimo koji je napon veći, pa njega uporedimo sa σd.

npr. U slucaju da je: l1<l2 sledi da je σ1>σ2 pa ćemo dimenzionisanje izvršiti na osnovu uslova σ1≤σd.

Primer b: Kruta homogena greda vezana elastičnim štapovima. Podrazumevamo da se kruta greda težine Q ne deformiše, a da se elastični štapovi, koje treba dimenzionisati, neznatno deformišu, na osnovu čega možemo smatrati da se tačke B i D premeštaju u nove položaje B́’ i D́’ pravolinijskim kretanjem. Štapovi su istog poprečnog preseka čija je površina A, a dužine su im l1 i l2. Težina štapa, naravno, deluje na njegovoj sredini. Ovde imamo dve jednačine: zbir svih vertikalnih sila mora biti jednak nuli, prva jednačina, a druga je zbir svih momenata, na primer u odnosu na oslonac A. Nepoznatih imamo tri: sile u oba štapa i reakciju veze u osloncu A. Dodatnu jednačinu formiraćemo na osnovu sličnosti trouglova, jer slični trouglovi imaju proporcionalne stranice.

2.1 Za štap uklješten na oba kraja, aksijalno opterećen silom F, odrediti napone u presecima delova štapa. Napone izračunati u funkciji od datih dužina i površina poprečnih preseka, kao i date sile. ( R : σ1 =    ∙ F ,   σ2 =   ∙ F ).

2.2 Dimenzionisati štap promenljivog kružnog poprečnog preseka, uklješten na oba kraja i opterećen aksijalnom silom F = 130 kN, uz uslov da prečnik d1 bude dva puta veći od prečnika d2. Dati su podaci : l1 = 0.25 m , l2 = 0.75 m , σd = 106 N/m2.

( R : d2 ≥ 195,4 mm, usvaja se d2 = 196mm , d1 = 392 mm ).

Varijante za vežbu:

1. d1=1,8 d2, l1 = 0,75 m , l2 = 1 m 2. d1=1,5 d2, l1 = 1,2 m , l2 = 1 m

3. d1=1,2 d2, l1 = 1, m , l2 = 1,2 m

2.3 Dimenzionisati štap sa slike ako je F=120kN, σd= 6•107 N/m2, E=2•1011 N/m2, l1=1m, l2=2m, A2=1,4 A1

(R: d1=38,7 mm usvaja se d1=39mm i d2 =46 mm )

Varijante za vežbu:

1. A2=2 A1 , l1= l2 2. A2=1,5 A1 ,l1=1,5m l2=1m, 3. A2=1,75 A1 l1=0,75m l2=1,25m

2.4 Štap kružnog poprečnog preseka, uklješten na oba kraja, opterećen je silom F= 100kN, kao na slici. Ako je σd= 7•106 N/m2, odrediti d1 i d2 uvažavajući traženi uslov a) A1=1,2A2 b) A1=0,62 A2

(a R: d1=113,34mm usvaja se d1=114mm, d2=104mm)

(b R: d2=118,3mm usvaja se d2=119mm, d1=92mm)

2.5 Kruta homogena greda AC oslonjena je krajem A na nepokretni oslonac, a u tačkama B i C pridržavaju je elastični štapovi BD i CE, kružnog poprečnog preseka istog prečnika. Težina grede je Q, a dužina l. Odrediti sile u štapovima i dimenzionisati štap opterećen većom silom, ako je σd= 6•107 N/m2, E=2•1011 N/m2.

(a R: F1=200/3 kN, F2=400/3 kN, d2=0,0532m=53,2mm usvaja se d1=54mm=d2)

(b R: F1=20kN, F2=40kN, d2=0,0146m=14,6mm usvaja se d2=15mm=d1)

2.6 Kruta greda AB obešena je u tački D o šipku CD dužine l, a zglobno vezana u tački A. Na slobodnom kraju B opterećena je silom F. Ako je površina poprečnog preseka šipke CD Am2, izračunati pomeranje tačke B, smatrajući da se ona pomera vertikalno naniže

(R: fB=(1+b/a) 2F•l/E•A)

9. ZATEZANJE POD UTICAJEM SOPSTVENE TEŽINE

 Zamislićemo da smo odstranili donji deo dugačkog štapa uklještenog na gornjem kraju, do preseka S. Dejstvo odstranjenog dela štapa zamenićemo težinom tog dela

Gde je   specifična težina.

Napon koji se javlja u preseku S jednak je

Ako je presek S na donjem kraju štapa, onda je Z=  =>  min = 0.

Ako je presek S u uklještenju, onda je Z=0 =>  max= .

Najveći napon se javlja u uklještenju, odnosno uklještenje predstavlja kritičan presek. Napon linearno raste od slobodnog kraja prema uklještenju, što je prikazano na slici.

Slika 12

Ako na donjem kraju štapa deluje još i aksijalna sila F, napon u proizvoljnom preseku biće jednak 

Slika 13

Interesuje nas deformacija ovako napregnutog štapa. Prvo ćemo posmatrati štap opterećen samo svojom težinom i zamislićemo da je štap podeljen na tanke poprečne slojeve. Na svaki od tih slojeva deluje napon različitog inteziteta, pa se svaki sloj različito deformiše .

Deformaciju celog štapa odredićemo kao aritmetičku sredinu deformacije najmanje deformisanog i najviše deformiisanog sloja

Najmanje deformisan sloj nalazi se na slobodnom kraju štapa i njegova deformacija je εmin=0. Najviše deformisan sloj nalazi se u uklještenju, a njegove deformacija je

Odatle sledi da je neka srednja deformacija

Kako je   to znači da je apsolutno izduženje štapa  . Ovaj izraz se može još malo transformisati

U slučaju kada na štap deluje još i aksijalna sila, apsolutno izduženje je

tj.       

10. UTICAJ TEMPERATURE NA NAPONE

Metalni štap izložen promeni temperature menja svoju dužinu, a nova dužina može se izračunati pomoću izraza l=l0(1+αΔT), gde je α koeficijent linearnog toplotnog širenja,a ΔT promena temperature, tj. ΔT=T2-T1 [°K]

Oslobodićemo se zagrada l=l0+l0αΔT

Kako je, inače, l=l0+Δl , možemo zaključiti da je izduženje štapa Δl=l0αΔT.

Toplotna dilatacija je εT= Δl/l0= αΔT.

Ako posmatramo uklješten metalni štap čije je izduženje usled povećanja temperature onemogućeno, u njemu će se javiti napon, kao da je aksijalno pritisnut

ZADACI

3.1 Železničke šine postavljene su pri temperaturi t1=10°C sa zazorom a=4mm. Dužina šine je

l 0=12,5m, koeficijent toplotnog širenja α=12,5•10-6 1/K°, modul elastičnosti E=2•1011 N/m2.

a) Koliki će biti zazor na temperaturi t2=-30°C?

b) Pri kojoj temperaturi će zazor nestati?

c) Koliki će biti napon u šinama na temperaturi t3=50°C?

(R: a) a1=10,25mm b) t=35,6°C c) σ=36MN/m2)

3.2 Vrh poluge dužine 1 cm termostata (A), na parnom kotlu , udaljen je od poluge ventila sigurnosti (B) za zazor a=0,1mm. Pri porastu temperature u kotlu poluga (A) se izdužuje i pomera polugu (B) nasuprot sile u opruzi (C), koja je tako podešena da se ventil sigurnosti otvori kada napon u poluzi (A) dostigne vrednost od 20KN/m2. Ako su karakteristike poluge (A) α=2•10-4 1/K° i E= 2•106 N/m2, izračunati koliko treba da poraste temperature u kotlu, da bi se ventil otvorio.

(R: ΔT=100°K)

3.3 Dimenzionisati čelični štap (γ=76518kg/m3, σd= 6•107 N/m2) dužine 20m, uklješten na gornjem kraju, opterećen sopstvenom težinom i silom zatezanja od 500kN na donjem kraju. Štap je cev:

a) kružnog poprečnog preseka, spoljašnjeg prečnika 25cm

b) kvadratnog poprečnog preseka, spoljašnje stranice a=20cm

(R: a) du=227 mm b) b=177 mm)

11. SMICANJE

Do smicanja dolazi u slučaju da na telo deluju dve sile istog pravca i intenziteta a suprotnog smera, čije su napadne linije na veoma malom rastojanju.

F

F

Slika 15.

Nacrtaćemo uveličanu sliku mesta na kojem dolazi do smicanja.

Slika 16.

a-razmak izmedju napadnih linija sila

∆s-pomeranje jednog dela tela u odnosu na drugi

γ-klizanje (deformacija kod smicanja)

Već smo rekli da posmatramo samo male deformacije. To znači da posmatramo samo male uglove, a za male uglove važe sledeća uprošćenja (kao dovoljno tačna).

sinα≈α i cosα≈1

a odatle sledi da je i tgα≈α

Ako ovo uprošćenje primenimo na primer smicanja, dobićemo:

tgα=∆s⁄a≈γ

Kod smicanja se javlja tangencijalni napon koji izračunavamo prema izrazu

τ=F/A

U ovom izrazu A je površina smicanja.U praktičnim primerima je od velike važnosti tačno odrediti po kojoj površini dolazi do smicanja i kakvog je oblika ta površina, jer od toga zavisi i kako ćemo je izračunati.

I za smicanje važi Hukov zakon, ali u obliku

τ=Gγ

G je modul klizanja koji je sa modulom elastičnosti povezan sledećim izrazom

G=E/2(1+ν)

Za metale modul klizanja je priblizno jednak 3/8 modula elastičnosti.

Neki primeri smicanja

1) Zakovice

2) Klin

Pre nego što proučimo slučaj klina, pogledaćemo slučaj otvora u limu:

Na ploču delujemo probojcem kružnog poprečnog preseka prečnika d. On će iz ploče istisnuti deo takodje kružnog poprečnog preseka.

Do smicanja je došlo po šrafiranoj površini, a ta površina je zapravo površina omotača valjka.

Kod klina njegovo telo teži da pod uticajem sile sa sobom ponese i deo glave koji je istog oblika kao i telo.

ZADACI

4.1 Nožem kvadratnog poprečnog preseka, stranice a=2cm, prosecaju se otvori na limu debljine 0,5cm. Kolikom silom treba delovati na nož, ako je  ?

(R: F 56kN)

4.2 Da li ekser prečnika 2mm, ukucan u zid, može držati sliku mase 10kg?  ?

(R: bio bi dovoljan i ekser prečnika d 1,25mm)

4.3 Na klin prečnika tela d=113mm, deluje sila F=80kN. Odrediti potrebnu debljinu glave klina ako je dozvoljeni napon  .

(R: h 37,56mm usvaja se h=38mm)

4.4 U limu debljine δ=2cm probijaju se kružni otvori prečnika 5cm. Kolikom silom treba delovati na probijač, ako je dozvoljeni napon na smicanje za lim τd=5•108 N/m2.

(R: F≥1,57MN)

4.5 Ploča težine 1kN pričvršćena je za vertikalan zid sa četiri vijka. Odrediti prečnik vijka ako je dozvoljeni napon materijala vijka τd=2•106 N/m2.

(R: d≥12,62mm usvaja se d=13mm)

4.6 U rezervoaru vlada pritisak p=106Pa. Poklopac rezervoara pričvršćen je sa 16 vijaka. Odrediti potreban prečnik vijka ako je σd=8•107 N/m2 i τd=7•107 N/m2 za materijal vijka, a prečnik rezervoara je D=2m.

(R: a) d≥59,8mm usvaja se d=60mm b) d≥55,9mm usvaja se d=56mm)

4.7 Kolika je sila potrebna da se preseče čelično uže od 24 žice, svaka je prečnika 3mm, ako je τd=8•107 N/m2?

(R: F≥13,57kN)

4.8 Kolika dužina lima, debljine 10mm, može biti isečena hidrauličkim makazama na koje deluje sila od 5MN, ako je τd=7•107 N/m2?

(R: l≥7,14m)

4.9 Odrediti prečnik stabla klina i debljinu njegove glave, ako je klin opterećen silom F=100kN, a dozvoljeni naponi su: τd=6•107 N/m2 i σd=8•107 N/m2.

(R: d≥46,1mm usvaja se d=47mm, h≥8,5mm usvaja se h=9mm)

4.10 Na kratku konzolu prečnika d okačeno je telo debljine δ i širine a, opterećeno silom F=150kN. Ako je a=20cm, τd=6•107 N/m2 i σd=8•107 N/m2, odrediti dimenzije δ i d.

(R: d≥48,9mm usvaja se d=49mm, δ≥16,6mm usvaja se δ=17mm)

4.11 Za telo na slici odrediti dimenzije a i d, ako su poznati podaci:

b=300mm, F=100kN, σd=8•106 N/m2 i τd=6•106 N/m2.

(R: d≥103mm, a=145mm, usvojeno)

4.12 Za telo na slici odrediti dimenzije l i d, ako su poznati podaci: F=100kN, D=200mm, σd=8•106 N/m2 i τd=6•106 N/m2.

(R: d≥103mm, l=129mm, usvojeno)

4.13 Klin opterećen silom F=15kN, stablom prolazi kroz otvor kružne ploče prečnika D=0,5m. Ploča je pričvršćena za zid dugačkim vijcima prečnika d2. Odrediti dimenzije klina d1 i h, prečnik vijka d2, i potreban broj vijaka ako su oni rasporedjeni po pločI tako da je rastojanje izmedju svaka dva vijka približno 3•d2. σd=8•106 N/m2, τd=6•106 N/m2.

(R: d1≥ 0,0489m usvaja se d1=49 mm, h≥0,0169 m usvaja se h=17 mm, d2≥0,0046m, usvaja se d2≥mm, n=104,2 usvaja se n=105)

12. GEOMETRIJSKE KARAKTERISTIKE POPREČNOG PRESEKA NOSAČA

Kod aksijalnog naprezanja, kao i kod smicanja, površina poprečnog preseka tela predstavlja meru sposobnosti tog tela da se suprotstavi deformisanju. Što je površina poprečnog preseka veća, to je napon manji. I u slučajevima savijanja, uvijanja i izvijanja, nosač koji ima veću površinu poprečnog preseka je sposobniji da izdrži opterećenje. Medjutim, kod ovih vrsta naprezanja površina poprečnog preseka nije jedini faktor značajan za otpornost tela. Bitnu ulogu imaju i oblik poprečnog preseka, kao i njegov položaj u odnosu na osu oko koje se vrši savijanje ili uvijanje. Svi ovi faktori obuhvaćeni su pojmovima: moment inercije i otporni moment.

Prvi pojam koji ćemo objasniti spada, zapravo, u oblast statike i nema neku praktičnu primenu u problemima kojima ćemo se baviti. To je statički moment površine.

Posmatramo ravan poprečni presek proizvoljnog oblika, koji ćemo podeliti na n elementarnih površina.

Statički moment ove figure je algebarski zbir proizvoda elementarnih površina i njihovih udaljenosti od x ili y ose.

Osa koja prolazi kroz težište ravne figure naziva se težišna osa.

Statički moment za težišnu osu jednak je nuli.

Na donjim slikama prikazani su neki slučajevi kod kojih su statički momenti jednaki nuli.

Sx=0

Sy=0                                                   Sx=Sy=0

MOMENTI INERCIJE

Momente inercije delimo na:

1.Aksijalne

2.Centrifugalne

3.Polarne

Aksijalni moment inercije površine poprečnog preseka (sa oznakom Ix ili Iy) za osu koordinatnog sistema jednak je algebarskom zbiru proizvoda elementarnih površina i kvadrata njihovog rastojanja od odgovarajuće koordinatne ose.

 tj. 

Aksijalni moment inercije ne može biti negativan ili jednak nuli.

Centrifugalni moment inercije površine poprečnog preseka za ose koordinatnog sistema jednak je algebarskom zbiru proizvoda elementarnih površina i njihovih rastojanja od obe koordinatne ose.

Centrifugalni moment može biti pozitivan, negativan ili jednak nuli. Zapravo, veoma je važno zapamtiti da je centrifugalni moment inercije jednak nuli ako je makar jedna od osa za koje je izračunat istovremeno i osa simetrije posmatrane figure.

Polarni moment inercije površine poprečnog preseka jednak je algebarskom zbiru proizvoda elementarnih površina i kvadrata njihovih rastojanja od koordinatnog početka.

Polarni moment se može izračunati, ako znamo aksijalne momente, kao njihov zbir

Momenti inercije izračunati za težišne ose nazivaju se sopstveni momenti inercije.

13. HAJGENS-ŠTAJNEROVA TEOREMA

Sopstveni momenti inercije za različite oblike poprečnih preseka tela izračunati su primenom elemenata više matematike i daju se u obliku tablica. Medjutim, u toku praktičnih izračunavanja javlja se potreba da se nadju momenti inercije za neke druge ose, koje nisu težišne. Ukoliko su te ose paralelne sa težišnim osama, njihovi momenti inercije mogu se izračunati primenom Hajgens-Štajnerove teoreme.

Posmatramo poprečni presek proizvoljnog oblika, sa težištem u tački C. Neka su sopstveni momenti inercije ove figure (Ix, Iy i Ixy) poznati.

Imamo potrebu da nadjemo momente inercije za neki drugi par osa,   i  , koje su paralelne sa osama X i Y.

Po definiciji, moment inercije za osu   naćićemo pomoću izraza

Na isti način dobija se

Proizvod  , odnosno  , naziva se položajni moment inercije za osu   (ksi), odnosno  (eta).

Dakle, moment inercije za osu paralelnu težišnoj jednak je zbiru sopstvenog momenta inercije i položajnog momenta – to je Hajgens Štajnerova teorema.

Primetimo samo da je   rastojanje izmedju paralelnih osa (x i ξ), a   rastojanje izmedju osa z i η.

Teorema važi i za centrifugalni, kao i za polarni moment inercije:

 i 

Otporni momenti

Kada znamo momente inercije, pomoću njih možemo naći otporne momente – aksijalne   i  , i polarni  . Ovi momenti su važni za praktične proračune jer pretstavljaju meru sposobnosti tela da se suprotstavi deformisanju pri savijanju ili uvijanju.

Aksijalni otporni momenti (koriste se kod savijanja i izvijanja) izračunavaju se na sledeći način:

,  , gde su   i   koordinate tačke koja je najudaljenija od x odnosno y ose. Pomoću njih se, dalje, izračunavaju naponi usled savijanja oko x ili z ose:

 i  .

Polarni otporni moment  koristi se kod uvijanja za izračunavanje tangencijalnog napona

.

Tablica momenata inercije

ZADACI

5.1 Izračunati momente inercije pravougaonika na slici (aksijalne, cenntrifugalni i polarni) za ose u i v.

Težišni momenti inercije za pravougaonik (podaci iz tablica) su

 i 

5.2 Odrediti, u funkciji od stranice b, aksijalne otporne momente (Wx,Wy) i polarni otporni moment Wo za sledeće oblike poprečnih preseka

5.3 Za oblik poprečnog preseka prikazan na slici, odrediti aksijalni (Wx) i polarni(Wo) otporni moment u funkciji od d i t, ako je b=0,5 t. Napomena: radi jednostavnosti, isečeni deo posmatrati kao pravougaonik stranica b i t.

5.4 Izračunati težišne momente inercije i njima pripadajuće otporne momente za sledeće oblike poprečnih preseka, ako je a=12cm.

5.5 Izračunati težišne momente inercije i njima pripadajuće otporne momente za sledeće oblike poprečnih preseka, ako je a=6cm.

Glavni momenti inercije

Ako pogledamo tablicu momenata inercije za različite figure, možemo primetiti da kod nekih figura nije napisan izraz za centrifugalni moment inercije – kod pravougaonika, kvadrata, kruga i polovine kruga. Nije napisan zato što je jednak nuli, a jednak je nuli zato što je jedna (ili obe ose) istovremeno i osa simetrije figure. Kod pravougaonika, kvadrata i kruga to su i x i y osa, a kod polovine kruga to je y osa.

Kod četvrtine kruga i pravouglog trougla postoji izraz za centrifugalni moment – zato što ni x ni y osa nisu ose inercije, centrifugalni moment nije jednak nuli, već je pozitivan ili negativan, zavisno od položaja figure.

Posmatrajmo, na primer, četvrtinu kruga. Kroz njeno težište mogu da se postave ne samo x-y osa, nego i još beskonačno mnogo parova osa koje sa x-y osama zaklapaju najrazličitije uglove. Da li medju njima postoji makar jedan par osa za koje bi centrifugalni moment inercije bio jednak nuli? Postoji i nije ga teško naći – osa-simetrala (u) ugla od 90 stepeni bila bi istovremeno i osa simetrije.

Ovaj par težišnih osa (u-v) za koje je centrifugalni moment jednak nuli, naziva se glavne centralne ose inercije. Dogovor je da takve ose ne obeležavamo slovima nego oznakama (1) i (2).

Zašto su ove ose važne? Za svaki par osa koje se seku u težištu postoje i odgovarajući momenti inercije, koji su svi medjusobno različiti i koje, zasad, ne možemo izračunati. Znamo, medjutim, da je moment inercije   koji odgovara osi (1) veći od svih njih, a moment  , koji odgovara osi (2), od svih najmanji. Oni, dakle, imaju ekstremne vrednosti. Što znači da će ova figura pri savijanju oko ose (1) pružiti najveći otpor, a pri savijanju oko ose (2) najmanji.

Momenti inercije   i   nazivaju se glavni centralni momenti inercije i mogu se izračunati pomoću izraza:

Takođe, kada znamo momente   i   možemo izračunati koji ugao glavne centralne ose zaklapaju sa osama x i y pomoću izraza

a koja je osa (1), a koja (2), pomoću ovih grafičkih pravila:

Hajde da primenimo ove izraze na četvrtinu kruga, usvojivši da mu je poluprečnik 2 cm:

S obzirom da je  veći od  , a   negativno, odgovara gornja leva sličica iz grafičkih pravila. Izračunaćemo i ugao

Svaka figura ima makar jedan par glavnih centralnih osa koje se, za figure koje nisu osno simetrične, mogu naći izračunavanjem, a za osno simetrične figure dovoljno je uzeti neku osu simetrije kao glavnu centralnu osu inercije.

Kod kruga je svaka osa koja prolazi kroz centar istovremeno i osa simetrije, što znači da krug ima beskonačno mnogo glavnih centralnih osa inercije. Kod kvadrata možemo uočiti dva para takvih osa, pri čemu su momenti inercije za obe ose medjusobno jednaki. To opet znači da je kod kvadrata i svaki drugi par osa koje se seku u težištu takodje par glavnih centralnih osa – po tome su krug i kvadrat slični.

Sada možemo definisati nov pojam – poluprečnik elipse inercije.

Poluprečnik   se nanosi na osu (2), a poluprečnik   na osu (1). Kada znamo poluprečnike elipse inercije možemo konstruisati elipsu inercije, koja se naziva centralna elipsa inercije ako su joj poluprečnici izračunati za glavne centralne ose inercije. Pomoću elipse inercije možemo naći, računskim ili grafičkim postupkom, moment inercije za bilo koje ose koje se seku u težištu figure.

Grafički postupak nije neshvatljiv, ali treba umeti konstruisati elipsu, pa ćemo to ovde preskočiti i navesti izraze pomoću kojih se, za ose koje sa glavnim centralnim osama zaklapaju neki ugao β, mogu izračunati njihovi momenti inercije:

Primer

Rešićemo, za primer, prvi zadatak sa ispita iz Otpornosti materijala I sa Građevinskog fakulteta iz septembra 2014.

Zašto da rešavamo zadatak za fakultet i zašto baš sa Građevinskog fakulteta?

Evo zašto: videćemo da i jedan solidan srednjoškolac može makar nešto da uradi na fakultetskom ispitu i time steći svest da je ovo što sada učimo deo jednog univerzalnog i primenljivog znanja i da se isplati, za sve koji planiraju da nastave neke studije tehnike, uložiti danas određeni trud da bi se to sutra vratilo kao pametno ulaganje.

Otpornost materijala se u nekom vidu izučava na većini tehničkih visokih škola i fakulteta, a najdetaljnije se izučava na Mašinskom fakultetu, kroz Otpornost materijala i Otpornost konstrukcija, i na Građevinskom fakultetu, kroz otpornost materijala I i II. Pri čemu je to izučavanje na Građevinskom fakultetu detaljnije i, čini mi se, napornije, nego na Mašinskom. Dakle, uzeli smo zadatak sa „najgoreg mogućeg mesta“.

Zadatak glasi:

Za poprečni presek nosača prikazan na slici odrediti glavne momente inercije, pravce glavnih osa inercije, poluprečnike inercije i skicirati elipsu inercije.

Zadatak ćemo prvo rešiti „peške“, tj. računaćemo sve po redu kao što smo i učili, što je u suštini obimno i dosadno, zahteva dosta vremena, ali je zato sigurno.

A da bi nam to bilo još opširnije i dosadnije, usput ćemo još i isprobavati kojekakve ideje i kroz njih izbrusiti dosadašnje znanje.

Bilo kako bilo, prvo ćemo sagledati kako sve može ova složena figura da se podeli na prostije delove.

Hajde da je, zasad, prikažemo na dva načina, oba pomoću jednakokrakih pravouglih trouglova.

Odlučimo se, recimo, za desnu sliku. Sada nam je zadatak da odredimo gde je težište figure. To je u suštini jasno već na prvi pogled, ali ćemo mi uvesti dve pomoćne ose i ipak težište odrediti starim dobrim računanjem. Zašto sam ose postavio baš ovako, i zašto sam ih označio baš sa Z i Y? Recimo da to i nije od neke presudne važnosti. Pređimo na računanje.

Dakle, ose koje smo ucrtali kao pomoćne, ostaju, jer im je koordinatni početak baš u težištu figure. To su težišne ose figure i koristićemo ih za pronalaženje glavnih momenata i glavnih osa inercije. Za taj posao nam trebaju momenti inercije figure u odnosu na Z i Y osu. A za momente inercije figure trebaju nam momenti inercije njenih delova u odnosu na njihove sopstvene težišne ose (one male ose ucrtane u težištima delova, T1 i T2). Znamo li te momente inercije? Pa, ja ih ne znam niti mi se kopa po tablicama. Ali, ništa zato, malo ćemo komplikovati i rešiti problem. Poćićemo od činjenice da je svaki od ovih naših jednakokrakih pravouglih trouglova zapravo polovina kvadrata. Znamo li sopstvene momente inercije kvadrata? To bi, ipak, trebali da znamo

.

Ali, šta ako kvadrat ima ovakav položaj:

Momenti inercije ostaju isti, a evo i zašto.

U oba položaja kvadrata, koordinatne ose su istovremeno i ose simetrije. To znači da je u oba položaja kvadrata centrifugalni moment inercije jednak nuli. A to opet znači da su ose Y i Z, u oba položaja, glavne centralne ose inercije, a momenti inercije koji su za njih izračunati su glavni centralni momenti inercije i moraju biti jednaki. Kvadrat je u tom pogledu kao kružnica: kako god da postavimo ose sa početkom u težištu, te ose će biti glavne centralne ose inercije.

Naš pravougli jednakokraki trougao je polovina tog kvadrata, pa ćemo mu momente inercije izračunati na sledeći način: moment inercije trougla koji tražimo jednak je razlici momenta inercije kvadrata i momenta inercije trougla koji je iz njega isečen (a koji je jednak momentu inercije koji tražimo).

Naša složena figura se sastoji od dva ovakva trougla, raspoređena sa različitih strana ose Z, pa je njihov ukupan moment inercije za tu osu jednak zbiru njihovih pojedinačnih momenata inercije

E sad, ovo smo mogli da izračunamo i na jedan mnogo elegantniji način, koji do sada nismo znali, a koji se zasniva na sledećim činjenicama:

a) Moment inercije neke figure u odnosu na osu (Y) se ne menja ako se figura pomera u pravcu ose (tj. translira se). 

b) Moment inercije neke figure u odnosu na osu (Y) se ne menja ako figuru preslikamo u odnosu na tu osu kao osu simetrije. 

c) Moment inercije neke figure u odnosu na neku osu (Y) se ne menja ako figuru preslikamo u odnosu na osu normalnu na osu Y. 

Ovo znači da smo, da bi izračunali moment inercija naše složene figure u odnosu na osu Z, mogli jednostavno da gornji trougao pomerimo na dole i dobijemo kvadrat. Dakle, moment inercije figure za Z osu je

      ili      

Dalje treba da izračunamo moment inercije za Y osu. Za taj posao nam treba moment inercije pravouglog trougla u odnosu na našu osu, a da bi smo to našli, treba nam moment inercije pravouglog trougla u odnosu na njegovu težišnu osu koja je paralelna Y osi. Za tu osu (prolazi kroz tačku T1), moment inercije je, istom logikom koju smo primenili i za Z osu:

Moment inercije jednog takvog trougla za Y osu naćićemo primenom Hajgens-Štajnerove teoreme:

Moment inercije cele figure jednak je zbiru momenata inercije dva trougla koja imamo i iznosi