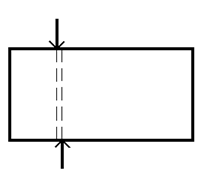
SMICANJE

Do smicanja dolazi u slučaju da na telo deluju dve sile istog pravca i intenziteta a suprotnog smera, čije su napadne linije na veoma malom rastojanju.

Nacrtaćemo uveličanu sliku mesta na kojem dolazi do smicanja.

a-razmak izmedju napadnih linija sila

∆s-pomeranje jednog dela tela u odnosu na drugi

γ-ugao klizanja (deformacija kod smicanja)

Već smo rekli da posmatramo samo male deformacije. To znači da posmatramo samo male uglove, a za male uglove važe sledeća uprošćenja (kao dovoljno tačna).

sinα≈α i cosα≈1

a odatle sledi da je i tgα≈α

Ako ovo uprošćenje primenimo na primer smicanja, dobićemo:

tgα=∆s⁄a≈γ

Kod smicanja se javlja tangencijalni napon koji izračunavamo prema izrazu

τ=F/A

U ovom izrazu A je površina smicanja.U praktičnim primerima je od velike važnosti tačno odrediti po kojoj površini dolazi do smicanja i kakvog je oblika ta površina, jer od toga zavisi i kako ćemo je izračunati.

I za smicanje važi Hukov zakon, ali u obliku

τ=Gγ

G je modul klizanja koji je sa modulom elastičnosti povezan sledećim izrazom

G=E/2(1+ν)

Za metale modul klizanja je priblizno jednak 3/8 modula elastičnosti.

Neki primeri smicanja

1) Zakovice

2) Klin

Pre nego što proučimo slučaj klina, pogledaćemo slučaj otvora u limu:

Na ploču delujemo probojcem kružnog poprečnog preseka prečnika d. On će iz ploče istisnuti deo takodje kružnog poprečnog preseka.

Do smicanja je došlo po šrafiranoj površini, a ta površina je zapravo površina omotača valjka.

ZADACI

4.1 Nožem kvadratnog poprečnog preseka, stranice a=2cm, prosecaju se otvori na limu debljine 0,5cm. Kolikom silom treba delovati na nož, ako je ?

(R: F 56kN)

4.2 Da li ekser prečnika 2mm, ukucan u zid, može držati sliku mase 10kg? ?

(R: bio bi dovoljan i ekser prečnika d 1,25mm)

4.3 Na klin prečnika tela d=113mm, deluje sila F=80kN. Odrediti potrebnu debljinu glave klina ako je dozvoljeni napon .

(R: h 37,56mm usvaja se h=38mm)

4.4 U limu debljine δ=2cm probijaju se kružni otvori prečnika 5cm. Kolikom silom treba delovati na probijač, ako je dozvoljeni napon na smicanje za lim τd=5•10⁸ N/m2.

(R: F≥1,57MN)

4.5 Ploča težine 1kN pričvršćena je za vertikalan zid sa četiri vijka. Odrediti prečnik vijka ako je dozvoljeni napon materijala vijka τd=2•106 N/m2.

(R: d≥12,62mm usvaja se d=13mm)

4.6 U rezervoaru vlada pritisak p=106Pa. Poklopac rezervoara pričvršćen je sa 16 vijaka. Odrediti potreban prečnik vijka ako je σd=8•107 N/m2 i τd=7•107 N/m2 za materijal vijka, a prečnik rezervoara je D=2m.

(R: a) d≥59,8mm usvaja se d=60mm b) d≥55,9mm usvaja se d=56mm)

4.7 Kolika je sila potrebna da se preseče čelično uže od 24 žice, svaka je prečnika 3mm, ako je τd=8•107 N/m2?

(R: F≥13,57kN)

4.8 Kolika dužina lima, debljine 10mm, može biti isečena hidrauličkim makazama na koje deluje sila od 5MN, ako je τd=7•107 N/m2?

(R: l≥7,14m)

4.9 Odrediti prečnik stabla klina i debljinu njegove glave, ako je klin opterećen silom F=100kN, a dozvoljeni naponi su: τd=6•107 N/m2 i σd=8•107 N/m2.

(R: d≥46,1mm usvaja se d=47mm, h≥8,5mm usvaja se h=9mm)

4.10 Na kratku konzolu prečnika d okačeno je telo debljine δ i širine a, opterećeno silom F=150kN. Ako je a=20cm, τd=6•107 N/m2 i σd=8•107 N/m2, odrediti dimenzije δ i d.

(R: d≥48,9mm usvaja se d=49mm, δ≥16,6mm usvaja se δ=17mm)

4.11 Za telo na slici odrediti dimenzije a i d, ako su poznati podaci:

b=300mm, F=100kN, σd=8•106 N/m2 i τd=6•106 N/m2.

(R: d≥103mm, a=145mm, usvojeno)

4.12 Za telo na slici odrediti dimenzije l i d, ako su poznati podaci: F=100kN, D=200mm, σd=8•106 N/m2 i τd=6•106 N/m2.

(R: d≥103mm, l=129mm, usvojeno)

4.13 Klin opterećen silom F=15kN, stablom prolazi kroz otvor kružne ploče prečnika D=0,5m. Ploča je pričvršćena za zid dugačkim vijcima prečnika d2. Odrediti dimenzije klina d1 i h, prečnik vijka d2, i potreban broj vijaka ako su oni rasporedjeni po pločI tako da je rastojanje izmedju svaka dva vijka približno 3•d2. σd=8•106 N/m2, τd=6•106 N/m2.

(R: d1≥ 0,0489m usvaja se d1=49 mm, h≥0,0169 m usvaja se h=17 mm, d2≥0,0046m, usvaja se d2≥mm, n=104,2 usvaja se n=105)