ZADACI – AKSIJALNO NAPREZANJE

1.1 Odrediti prečnik štapa kružnog poprečnog preseka opterećenog na istezanje silom F=100kN, ako je dozvoljeni napon σ_d= 8•10⁷N/m²

(R: d=39,9mm usvajamo d=40mm)

Varijante za vežbu:

1. F=120 kN, σd=10⁷N/m²

2. F=80 kN, σd=8•10⁶N/m2

1.2 Štap kvadratnog poprečnog preseka opterećen je na pritiskivanje silom F= 80kN. Odrediti stranicu a poprečnog preseka, ako je dozvoljeni napon σ_d= 6•10⁷N/m²

(R: a=36,5mm usvaja se a=37mm)

Varijante za vežbu:

1. F=100 kN, σ_d=2•10⁷N/m²

2. F=120 kN, σ_d=4•10⁷N/m²

1.3 Odrediti unutrašnji prečnik cevi kružnog poprečnog preseka opterećene aksijalnom silom F=80kN, ako je dozvoljeni napon σ_d= 6•10⁷N/m², a spoljašnji prečnik (d_s) je 12cm.

(R: du=112,7mm usvaja se du=112)

Varijante za vežbu:

1. F=100 kN, d_s=1,5 dm . 2. F=120 kN, d_s=0,2 m

1.4 Cev kvadratnog poprečnog preseka opterećena je aksijalnom silom F= 100kN. Odrediti spoljašnju stranicu poprečnog preseka (a), ako je unutrašnja stranica (b) 6cm, a dozvoljeni napon σ_d= 8•10⁷N/m²

(R: a=69,64mm usvaja se a=70mm)

1.5 Dimenzionisati aksijalno napregnutu cev od materijala čiji je dozvoljeni napon σ_d= 8•10⁷N/m², ako je:

a) cev kružnog poprečnog preseka, sila iznosi 100kN, a spoljašnji prečnik je za 10% veći od unutrašnjeg

Varijante za vežbu:

1. F=120 kN

2. F=80 kN

b) cev kvadratnog poprečnog preseka, sila iznosi 200kN, a unutrašnja stranica poprečnog preseka je za 10% manja od spoljašnje

Varijante za vežbu: 1. F=180 kN

2. F=210 kN

(a R: du=87,1 mm, usvaja se du=87mm, ds=95,81mm, usvaja se ds=96mm)

(b R: a=114,7mm, usvaja se a=115mm, b=103,23mm, usvaja se b=104mm)

1.6 Štap dužine lo=2m, pravougaonog poprečnog preseka, stranica a=0,1m i b=0,05m, izduži se pod dejstvom neke aksijalne sile za ∆l=0,0003m. Izračunati skraćenje stranica a i b, ako je Puasonov broj ν=1/3, i silu ako je modul elastičnosti E=2•1011N/m2.

(R: ∆a=-5•10-6m, ∆b=-2,5•10-6m, F=150kN)

1.7 Štap kvadratnog poprečnog preseka stranice a=0,1m, izduži se pod dejstvom sile F=100kN na dužinu l=2,2m. Izračunati početnu dužinu štapa ako je E=2•1011 N/m2

(R: lo=2,19989m)

1.8 Cev kružnog poprečnog preseka zategnuta je silom F=150kN. Dimenzionisati cev tako da debljina zida (δ) bude 1cm, ako je σd= 8•107 N/m2.

(R: du=49,68mm, usvaja se du=50mm, ds=70mm)

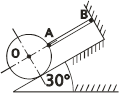
1.9 Dimenzionisati štap AB, kvadratnog poprečnog preseka, za čiji kraj A je pričvršćena kugla težine 80kN, ako je kugla oslonjena još i na kosu ravan. σd= 6•107 N/m2.

(R: a=25,82mm usvaja se a=26 mm)

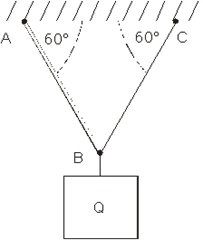
1.10 Teret težine Q=100kN okačen je na štap AB i uže BC kao na slici. Dimenzionisati štap AB, ako je σd=8•107 N/m2. Štap je kružnog poprečnog preseka.

 (R: d=30,3mm, usvaja se d=31mm)

Varijante za vežbu: 1. 

2. 

1.11 Kugla težine 60kN može biti okačena na dva predložena načina (a i b).

Odrediti potreban prečnik štapa AB, kružnog poprečnog preseka, za oba slučaja, ako je

dozvoljeni napon materijala štapa σd= 12•107 N/m2.

(a R: d=25,2m usvaja se d=26mm)

(b R: d=0,0271m usvaja se d=27mm)

1.12. Gredu težine Q=30kN, dužine l=2m pridržava čelično uže sastavljeno od n=24 žice, koje sa nepokretnom ravni zaklapa ugao od 60 stepeni.

Odrediti potreban prečnik žice ako je dozvoljeni napon σd = 8 ∙ 107 N/m2 .

( R : d ≥ 3,9 mm, usvaja se d = 4 mm ).

Varijante za vežbu: 1. Q=10000N, α=75°, n=10

2. Q=25 kN, α=15°, n=12

1.13 Teret Q okačen je kao na slici. Štap AC je čelični, prečnik mu je d1 = 30 mm, a σd1 = 16x 107 N/m2. Štap BC je od aluminijuma, d2 = 40 mm, a σd2 = 6 ∙ 107 N/m2. Koliki teret može da izdrži ova konstrukcija?

( R : Q ≤ 130,53 kN ).

1.14 Kugla težine Q = 60 kN oslonjena na glatku ravan nagiba 60° i na njoj paralelan drveni podupirač kvadratnog poprečnog preseka stranice a = 300 mm. Ako je dozvoljeni napon za materijal podupirača σd = 3  ∙ 104 N/m2, proveriti da li je napon u podupiraču u dozvoljenim granicama.

( R : σ = 0,33  ∙ 106 N/m2 > σd => NIJE. Stranica podupirača treba da bude a ≥ 1m )

1.15 Radni pritisak u cilindru parne masine p = 106 N/m2, a prečnik cilindra je D = 350 mm. Sa koliko zavrtnja prečnika d = 18 mm treba pričvrstiti poklopac cilindra ako je dozvoljeni napon za materijal zavrtnja σd = 4 kN/cm2 .

( R : n ≥ 9,45, usvaja se n = 10 ).

Varijante za vežbu:

1. p=2000 kN/m2, D=30 cm d=0,18cm, σd =4 ∙ 104 N/mm2

2. p=400 N/cm2, D=2,8 dm d=2 cm, σd =4 ∙ 104 daN/dm2

1.16 Telo težine Q = 50 kN nalazi se na hrapavoj ravni nagibnog ugla α=60° i koeficijenta trenja µ = 0,5 . U stanju mirovanja održava ga uže sastavljeno od n=20 žica. Odrediti prečnik žice ako je dozvoljeni napon za materijal žice

σd = 6 ∙ 108 N/m2 .

( R : d ≥ 1,8 mm, usvaja se d = 2 ).

Varijante za vežbu: 1. α=30°, µ = 0,25, n=10 2. α=45°, µ = 0,3, n=12

1.17 a) Odrediti potrebne dimenzije poprečnog preseka štapova opterećenih kao na slici, ako je dozvoljeni napon pri zatezanju σdZ = 6 ∙ 106 N/m2 a pri pritiskivanju σdP = 4 ∙ 106 N/m2. . Štap 1 je kružnog, a štap 2 kvadratnog poprečnog preseka (varijanta A ), a u varijanti B štap 1 je kvadratnog, a 2 kružnog poprečnog preseka.

b) Ako je dužina štapa 1  l0 = 4 m, Jungov modul elastičnosti E = 2 ∙ 10¹¹ N/m2 , Poasonov broj ν=1/3 , izračunati izduženje (skraćenje) štapa Δl, kao i promenu dimenzije poprečnog preseka (Δd za varijantu A, Δa za varijantu B).

Vrednosti uglova date su u tablici.