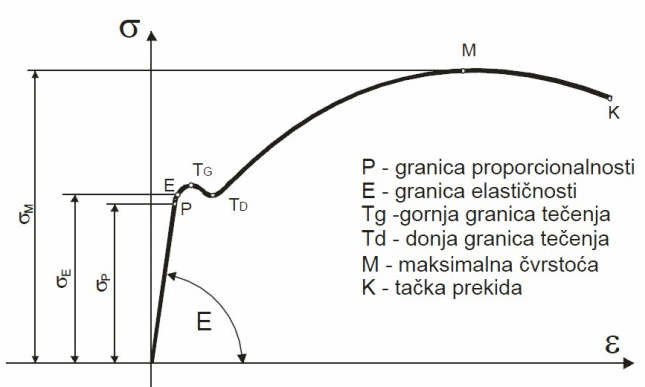
Hookov zakon opisuje ponašanje materijala u oblasti elastičnih deformacija. Sila koja deluje duž ose predmeta teži da izduži ili sabije taj predmet – javlja se relativna deformacija kao odnos izduženja (skraćenja) i početne dužine ε = ΔL / L. Sila u materijalu izaziva napon σ = F / A pa možemo posmatrati dijagram napon – deformacija, sa koga se lepo vidi da je u pocetku naprezanja zavisnost linearna sve do granice proporcionalnosti P, zatim prelazi u blagu krivu do granice elqstičnosti E. Nakon te granice, deformacije postaju plastične (ireverzibilne) i nisu nam od interesa za ovaj predmet. Samo valja pomenuti granicu tečenja (gornju i donju), maksimalnu čvrstoću i granicu loma

Do granice proporcionalnosti Hookov zakon ima linearni oblik, a do graice elastičnosti deformacije su reverzibilne (materijal se vraća u prvobitno stanje. Taj deo se naziva oblast elastičnosti, i sve zadatke ćemo bazirati na izučavanju opterećenja u toj oblasti. Za zadatke nam prvo treba tabela gde su za različite materijale date vrednosti Jungovog modula elastičnosti E, kao i granice elastičnosti σE. Modul elastičnosti (E) je teoretska veličina i predstavlja naprezanje potrebno da se materijal izduži za 100% svoje prethodne dužine (dakle naprezanje kada je ε=1. To se u praksi obično ne dešava (materijal pukne pre toga). Granica elastičnosti σE je ‘opipljiva’ veličina i definiše maksimalno naprezanje nakon kojeg se materijal vraća u prvobitni položaj.
Materijal |
Modul elastičnosti E [GPa] |
Granica elastičnosti σE [MPa] |
|---|---|---|
Čelik meki |
210 |
200–250 |
Čelik tvrđi |
210 |
300–400 |
Prohrom |
200 |
200–300 |
Aluminijum |
70 |
50–150 |
Bakar |
110 |
60–150 |
Mesing |
100 |
150–250 |
Liveno gvožđe |
100–120 |
100–200 |
Poliamid (PA) |
2–3 |
40–80 |
Drvo (duž vlakana) |
8–15 |
40–100 |
Osim ove tabele, koristićemo i osnovne formule iz Hookovog zakona istezanja
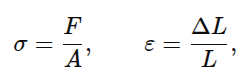
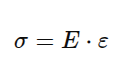
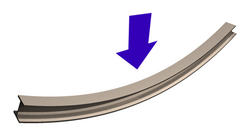
Definicija: Pojava kada na štap ili gredu deluje poprečno opterećenje, izazivajući zakrivljenje ose elementa.
Normalno naprezanje pri savijanju:
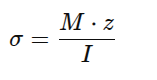
gde je M – moment savijanja, z – rastojanje od neutralne ose, I – moment inercije preseka. Kad se štap (greda) savija pod dejstvom momenta savijanja, u preseku nastaju naponi rastezanja i sabijanja.
Jedan deo preseka (iznad neutralne ose) je sabijen a drugi deo preseka (ispod neutralne ose) je istegnut.
Neutralna osa: linija u preseku gde nema naprezanja.
Praktični primeri: grede mostova, osovine pod teretom, elementi mašina.
Osnovni pojmovi o smicanju
Smicanje je naprezanje uzrokovano transverzalnom silom koja teži da poprečnim opterećenjem izazove klizanje materijala u pravcu delovanja sile.
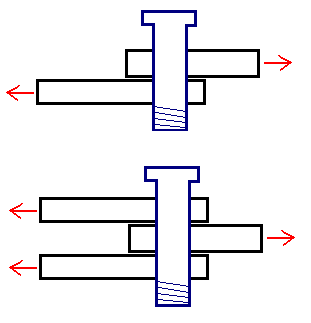
Smičuće naprezanje računamo po formuli
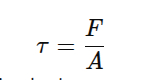
Praktični primeri: zakivci, klinovi, zavrtnji, osovine kod prenosa obrtnog momenta.
Otpornost materijala na smicanje, takođe poznata kao čvrstoća na smicanje, je sposobnost materijala da se odupre sili koja ga tera da se deformiše ili puca pod dejstvom transverzalnih (paralelnih) sila, koje deluju u suprotnim smerovima na različitim delovima materijala. Merna jedinica za čvrstoću na smicanje je isto kao i za pritisak ili napon, a to je Paskal (Pa) ili megapaskal (MPa), koji se izračunava kao odnos sile smicanja i površine poprečnog preseka.
Osnovni pojmovi o uvijanju (torziji)
Uvijanje (torziju) izaziva spreg sila koje deluju u ravni poprečnog preseka. Ove sile formiraju moment uvijanja.
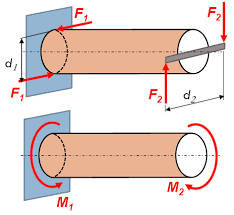
Opterećenje koje nastaje u materijalu je opterećenje smicanja (klizanje) i u svakoj tački preseka ono iznosi
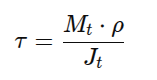
Gde je Mt moment torzije, ρ radijus do tačke u preseku a Jt je polarni moment inercije preseka. Ugao uvijanja se može izraziti formulom
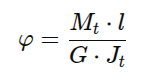
gde je G modul klizanja a l dužina štapa.