Stepeni slobode (DoF – Degrees of Freedom) označavaju broj nezavisnih kretanja koje kinematski par može da izvede. U trodimenzionalnom prostoru, telo može imati do šest stepeni slobode:
· Tri translaciona kretanja (duž X, Y i Z ose)
· Tri rotaciona kretanja (oko X, Y i Z ose)
Svaki kinematski par ograničava određene stepene slobode, čime se definiše vrsta kretanja koje omogućava:
· Obrtni par – 1 stepen slobode (rotacija oko jedne ose)
· Prizmatični par – 1 stepen slobode (translacija duž jedne ose)
· Cilindrični par – 2 stepena slobode (kombinacija translacije i rotacije)
· Sferni par – 3 stepena slobode (rotacija u svim pravcima)
Razumevanje stepena slobode je ključno za projektovanje robotskih sistema, jer određuje fleksibilnost i mogućnosti kretanja manipulatora.

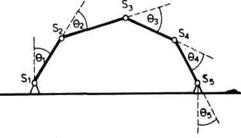
Kod zatvorenih lanaca problem je složeniji. Broj stepeni slobode lanca nije jednak broju zglobova. Posmatrajmo mehanizam prikazan na slici. Ovaj zatvoreni lanac ima pet zglobova, svaki sa po jednim rotacionim stepenom slobode. Za određivanje položaja ovog lanca potrebno je znati uglove, tj. dovoljno je znati dva parametra (zbog geometrijskih ograničenja uglova trougla). Dakle, lanac ima dva stepena slobode iako ima pet zglobova.
2.2.GEOMETRIJA MANIPULACIONIH ROBOTA
Sada ćemo sa opšte analize kinematičkih lanaca krenuti ka mehanizmima koji se javljaju u praktičnim realizacijama manipulacionih robota. Analiziraćemo strukturu "ruke" i "šake" robota. Zatim ćemo prodiskutovati broj stepeni slobode manipulacionog robota. Definisaćemo vektore koji određuju geometriju robota i na kraju pokazati postupak proračuna položaja mehanizma robota i položaja radnog predmeta.
2.2.1. Minimalna konfiguracija manipulacionog robota
Sl. 2.13. Minimalna konfiguracija i šaka robota
Minimalna konfiguracija podrazumeva mehanizam sa tri zgloba, odnosno tri stepena slobode. Na takvu minimalnu konfiguraciju nadovezuje se takozvani završni, mehanizam robota koji ćemo uslovno nazivati šaka. Na slici 2.13 shematski je predstavljena podela lanca na minimalnu konfiguraciju i šaku. Sledi da minimalna konfiguracija obuhvata zglobove S1,S2i S3i segmente 1, 2 i 3, a šaka se nadovezuje i sadrži određeni broj zglobova i segmenata (na primer 4, 5 i 6). Naziv minimalna konfiguracija potiče otuda što svaki manipulacioni robot poseduje takav mehanizam. Minimalna konfiguracija često se definiše kao mehanizam sa tri stepena slobode koji vrši pozicioniranje tj. dovođenje šake na željeno mesto u radnom prostoru. Kasnije ćemo videti da se pod pojmom pozicioniranja obično podrazumeva položaj samog vrha šake robota (tačka A na slici 2.13). Tako, na taj položaj, pored minimalne konfiguracije, utiču i segmenti same šake. Otuda se može reći da minimalna konfiguracija određuje položaj korena šake, (tačka C na slici 2.13), a zajedno sa šakom vrši pozicioniranje vrha (tačka A na slici 2.13).
Minimalna konfiguracija je mehanizam sa tri zgloba od kojih svaki može biti rotacioni ili translatorni. Označimo sa R rotacioni, a sa T translatorni zglob. Sada možemo uvesti označavanje mehanizma na sledeći način: na primer RTT označava mehanizam sa tri zgloba (i tri stepena slobode) od kojih je prvi rotacioni, a druga dva translatorna. Sada ćemo, koristeći uvedeno označavanje obraditi najčešće sheme minimalne konfiguracije robota.
a) Pravougaona ili TTT shema. Minimalna konfiguracija pravougaone ili TTT sheme ima tri translatorna zgloba. Na slici 2.14 prikazan je primer ovakve minimalne konfiguracije i to izgled robota i njegov shematski prikaz.
Sl 2.14. Pravougaona minimalna konfiguracija
Kako je na slici prikazano, minimalna konfiguracija se završava jednom pločicom (C na slici 2.14) na koju se zavrtnjima ili nekako drugačije vezuje šaka robota. Treba, ipak, naglasiti da minimalna konfiguracija i šaka ne moraju biti ovako odvojene celine. Vrlo često se i ne mogu fizički razdvojiti zato što se motori koji pokreću zglobove šake nalaze negde na segmentima minimalne konfiguracije, da bi bili bliže centralnom stubu i time manje opterećivali robot. Odatle se pogoni prenose prenosnom mehanizmom do zglobova šake. U ovakvim slučajevima podela na minimalnu konfiguraciju i šaku robota ima smisla samo shematski, a ne i na stvarnoj konstrukciji.
Posmatrajmo TTT-shemu prikazanu na slici 2.14 i razmotrimo šta je to što ograničava mogućnost da vrh C stigne u bilo koju tačku prostora. Ograničenje potiče otuda što je pomeranje bilo kog segmenta kroz odgovarajući zglob ograničeno. Na primer, kod klizanja zgloba S1 po šipki G1G2 uvedeni su mehanički graničnici (G1 i G2). I kod ostalih zglobova dužina izvlačenja ili uvlačenja segmenata ograničena je samom dužinom segmenata, pa se u konstrukciji uvode graničnici.
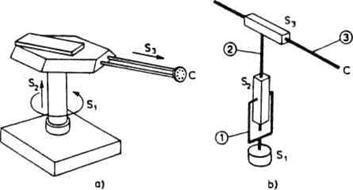
Sl. 2.16. Cilindrična minimalna konfiguracija
b) Cilindrična ili RTT-shema. Minimalna konfiguracija cilindrične ili RTT-sheme ima tri zgloba od kojih je prvi rotacioni, a druga dva translatorna. Na slici 2.16 prikazan je primer ovakve minimalne konfiguracije i to izgled robota i njegov shematski prikaz.
Naziv
cilindrična shema potiče otuda što pomeranja u zglobovima S1,
S2 i S3 tačno odgovaraju koordinatama
![]() ,Z i
,Z i
![]() cilindričnog koordinatnog sistema, što se vidi upoređivanjem
slike 2.16 i 2.17 (a).
cilindričnog koordinatnog sistema, što se vidi upoređivanjem
slike 2.16 i 2.17 (a).
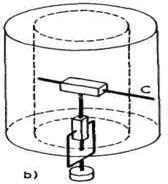
Sl. 2.17. Cilindrični koordinatni sistem i radni prostor
Razmotrimo sada radni prostor RTT-sheme robota. Ograničenja se ovde javljaju zbog ograničene dužine segmenta 2 i 3, te se oni mogu izvlačiti (odnosno uvlačiti) iz odgovarajućih zglobova samo do određene mere. Za obrtanje u zglobu S1 smatraćemo da nije ograničeno, mada i tu mogu da se pojave ograničenja. S obzirom na uvedena ograničenja, radni prostor cilindričnog robota izgledao bi kao na slici 2.17 (b).
c) Sferna ili RRT-shema,. Minimalna konfiguracija sferne ili RRT- sheme ima tri zgloba od kojih su prva dva rotaciona, a treći translatorni. Na slici 2.6 (b) prikazan je primer sfernog robota i njegova shema. Na slici 2.11 data je još jedna moguća shema sfernog robota. Treća moguća RRT- shema data je na slici 2.18 (a).
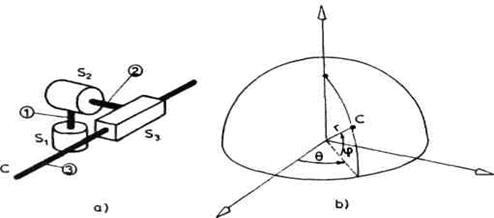
Sl. 2.18. Sferna minimalna konfiguracija
Pomeranja u zglobovima kod RRT-sheme približno odgovaraju koordinatama sfernog koordinatnog sistema (slika 2.18 b), pa otuda naziv sferna shema.