Pojam Koordinatnog Sistema

1. Uvod u kinematiku robota

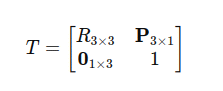
Kinematika robota bavi se proučavanjem pokreta robota – kako se njegovi delovi (npr. ruke, zglobovi) pomeraju u prostoru. Da bismo precizno opisali te pokrete, neophodno je da koristimo koordinatne sisteme. Oni nam pomažu da matematički zabeležimo položaj (gdje se nešto nalazi) i orijentaciju (kako je nešto okrenuto) robota ili njegovih delova.

2. Šta je koordinatni sistem?

Koordinatni sistem je način da pomoću brojeva opišemo položaj tačaka u prostoru. Najčešći sistem koji se koristi je kartesijanski koordinatni sistem.

• Kartesijanski koordinatni sistem:
  Svaka tačka u prostoru je opisana pomoću tri broja – x, y i z.
  Na primer, tačka P može biti predstavljena kao: P=(x,y,z)

Zamislite da je vaše školsko dvorište kao prostran prostor, a svaki predmet (drvo, klupa) se nalazi na određenoj lokaciji koju možemo opisati kao par (ili trojku) brojeva.

3. Vrste koordinatnih sistema u robotici

U robotici se koristi više koordinatnih sistema, a najčešće su:

1. Globalni (svetski) koordinatni sistem

   • To je fiksni sistem koji koristimo kao referencu za ceo prostor u kome robot radi.

   • Na primer, u fabrici možemo postaviti koordinatni sistem sa početkom u jednom uglu prostorije.

2. Lokalni koordinatni sistemi

   • Ovi sistemi su vezani za delove robota, kao što su baza robota, pojedinačni zglobovi ili krajnji efektor (robotova ruka).

   • Svaki lokalni sistem ima svoje koordinate, a pomoću njih možemo precizno opisati pokrete svakog dela robota.

3. Koordinatni sistem alata (end-effector)

   • Ovaj sistem je vezan za alat koji robot koristi (npr. robotska šaka).

   • Omogućava da se odredi kako je alat orijentisan u odnosu na objekat koji treba da se manipuliše.

4. Transformacije između koordinatnih sistema

Da bismo prešli iz jednog koordinatnog sistema u drugi, koristimo transformacije. Ovo je veoma važno, jer:

• Ako znamo položaj robota u lokalnom koordinatnom sistemu (npr. položaj jednog zgloba), moramo ga prevesti u globalni koordinatni sistem da bismo znali gde se robot nalazi u prostoriji.

• Transformacije kombinuju rotacije (promene orijentacije) i translacije (pomeranja).

Homogena matrica transformacije

Jedan od najčešćih načina da se opiše promena koordinatnih sistema je korišćenje homogene matrice transformacije. Ta matrica (dimenzija 4×4) kombinuje rotaciju i translaciju u jednu operaciju. Njena opšta forma izgleda ovako:

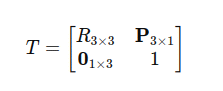
• R_3×3 predstavlja rotacionu matricu (opisujući orijentaciju).

• P_3×1 predstavlja vektor translacije (opisujući pomeranje).

• Korišćenjem ove matrice možemo prebaciti koordinate tačke iz jednog sistema u drugi.

5. Primer: Robotska ruka i Denavit-Hartenberg (DH) konvencija

Zamislite robotsku ruku sa nekoliko zglobova. Da bismo opisali položaj i orijentaciju krajnjeg efektora (npr. ruke koja hvata predmet), svakom zglobu dodeljujemo svoj lokalni koordinatni sistem.

Denavit-Hartenberg konvencija je sistematski metod za dodeljivanje ovih koordinatnih sistema, što omogućava da se izračunaju transformacije od baze robota do krajnjeg efektora.
Na taj način, lanac transformacija (od baze do ruke) možemo zapisati kao proizvod homogenih matrica, i time izračunati gde se tačno nalazi krajnji efektor u globalnom koordinatnom sistemu.

6. Zaključak

• Koordinatni sistemi su osnova za opisivanje položaja i orijentacije u prostoru.

• U robotici koristimo globalne i lokalne koordinatne sisteme da bismo precizno kontrolisali pokrete robota.

• Transformacije između koordinatnih sistema, naročito pomoću homogenih matrica, omogućavaju prelazak sa opisa pokreta u lokalnim okvirima na globalne opise.

• Razumevanje ovih pojmova je ključno za dalje proučavanje kinematike robota i pravilno programiranje njegovih pokreta.