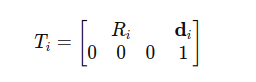
Direktna kinematika

Šta je direktna kinematika?

Direktna kinematika (eng. Forward Kinematics, FK) se bavi problemom određivanja položaja i orijentacije krajnjeg efektora (npr. ruke ili šake robota) kada su poznati svi parametri zglobova – kao što su uglovi kod rotacionih zglobova ili pomaci kod translacionih zglobova.

Kako se rešava direktna kinematika?

1. Modelovanje robota kao kinematičkog lanca:
   Robota zamišljamo kao lanac povezanih segmenata (linkova) i zglobova. Svaki zglob ima svoj lokalni koordinatni sistem, a odnos između uzastopnih koordinatnih sistema opisujemo pomoću transformacionih (homogenih) matrica.

2. Korišćenje transformacionih matrica:
   Za svaki zglob, definisemo homogenu matricu transformacije Ti​ koja kombinuje rotaciju i translaciju:

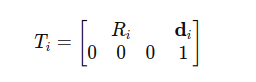
• Ri​ je rotaciona matrica koja opisuje orijentaciju segmenta.

• di​ je vektor translacije koji opisuje pomeranje do sledećeg zgloba.

1. Kompozicija transformacija:
   Konačna transformacija koja prelazi iz baze robota do krajnjeg efektora dobija se kao proizvod svih pojedinačnih matrica:

   Ttotal​=T1​⋅T2​⋅…⋅Tn​

   Iz matrice Ttotal​ možemo direktno pročitati:

   • Poziciju krajnjeg efektora (poslednja kolona, odnosno vektor P).

   • Orijentaciju (gornji levi 3×3 blok – rotaciona matrica).

Primer – Planarni (2D) robotski manipulator sa dva rotaciona zgloba:

Ako su dužine segmenata L1​ i L2​, a uglovi zglobova θ1​ i θ2​, položaj krajnjeg efektora (x,y) se računa kao:

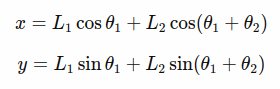
Ovaj primer ilustruje kako se pomoću poznatih zglobnih parametara (uglova) može odrediti položaj krajnjeg efektora – što je suština direktne kinematike.

Inverzna kinematika

Šta je inverzna kinematika?

Inverzna kinematika (eng. Inverse Kinematics, IK) predstavlja suprotan problem od direktne kinematike. Ovde je cilj: dat je željeni položaj i orijentacija krajnjeg efektora, pronaći vrednosti zglobnih parametara (npr. uglove kod rotacionih zglobova) koje će omogućiti da krajnji efektor dostigne tu konfiguraciju.

Zašto je inverzna kinematika složenija?

• Nelinearnost jednačina:
  Jednačine koje povezuju zglobne parametre sa položajem krajnjeg efektora su često nelinearne, što znači da se mogu pojaviti višestruka rešenja ili čak nijedno rešenje.

• Višestruka rešenja:
  Jedna i ista pozicija krajnjeg efektora može se dostići na više načina. Na primer, robotska ruka može imati konfiguraciju "lakat gore" ili "lakat dole" – oba rešenja su matematički validna.

• Fizička ograničenja:
  Robot možda ima mehanička ograničenja (ograničen raspon pokreta zglobova) koja dodatno komplikuju pronalaženje rešenja. Ako je traženi položaj izvan dometa robota, rešenje jednostavno ne postoji.

Metode rešavanja inverzne kinematike

1. Analitički pristupi:

   • Za jednostavnije robote (sa manje zglobova) moguće je dobiti tačne analitičke izraze za zglobne parametre.

   • Primer: planarni manipulator sa dva ili tri zgloba često ima zatvorene formule (kao što je gore pomenuti primer za direktnu kinematiku, ali "obrnuto").

2. Numerički pristupi:

   • Kod kompleksnijih robota (npr. sa 6 ili više stepena slobode), analitičko rešenje može biti izuzetno komplikovano ili čak nemoguće.

   • Tada se koriste iterativne metode, kao što su:

     • Newton-Raphson metoda

     • Jacobian pseudoinverse metoda
       Ove metode postepeno prilagođavaju vrednosti zglobnih parametara tako da se minimizira greška između željene i trenutne pozicije krajnjeg efektora.

3. Heuristički algoritmi:

   • U nekim slučajevima, posebno u realnom vremenu ili kod robota sa velikim brojem stepena slobode, koriste se optimizacione metode i algoritmi zasnovani na heuristikama kako bi se našlo "dovoljno dobro" rešenje.

Primena inverzne kinematike

• Planiranje puta:
  Kada robot treba da pređe iz jedne pozicije u drugu, inverzna kinematika pomaže da se izračunaju potrebni pokreti svakog zgloba za postizanje željene konfiguracije.

• Interakcija sa okolinom:
  Kod zadataka poput hvatanja objekata, robot mora da "razmisli" kako da postavi svoju ruku (krajnji efektor) tako da dohvati predmet, a inverzna kinematika omogućava to prevođenjem pozicije objekta u odgovarajuće zglobne parametre.

3. Zaključak

• Direktna kinematika je prilično „direktna“ – kada su poznati zglobni parametri, lako je izračunati gde se nalazi krajnji efektor.

• Inverzna kinematika je kompleksnija jer se bavi problemom pronalaženja zglobnih parametara za željenu poziciju i orijentaciju, pri čemu može doći do višestrukih ili nepostojećih rešenja.

• Razumevanje oba problema je ključno za pravilno programiranje i kontrolu robota u industrijskim, medicinskim i drugim primenama.