Uvod u pojam momenta inercije preseka

Moment inercije preseka predstavlja meru otpora preseka savijanju i uvijanju.
Što je moment inercije veći, element je krući, manje se deformiše pri opterećenju.

Za linijske preseke se koriste dva momenta inercije:

• Moment inercije oko x-ose: I_x

• Moment inercije oko y-ose: I_y

Postoji i polarni moment inercije preseka:

• I_p=I_x+I_y

Polarni moment se koristi kod uvijanja kružnih preseka.

Opšta ideja momenta inercije

Moment inercije „meri“ kako je površina raspoređena u odnosu na osu.
Što su delovi preseka udaljeniji od ose, to više doprinose momentu inercije.

Primera radi:

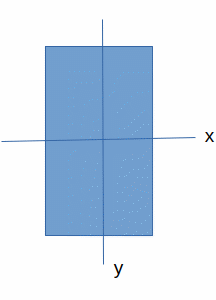
• Uska i visoka pločica ima veliki I_x (jer je visina daleko od ose x).

• Široka i niska pločica ima veliki I_y.

Osnovni geometrijski oblici i njihovi momenti inercije

Pravougaonik (A = b × h)

Presek dimenzija:

• širina: b

• visina: h

Momenti inercije oko osa koje prolaze kroz centar preseka:

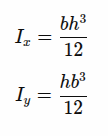
Napomena:
Kada računamo moment inercije oko ose x, kubira se visina; kada računamo oko y, kubira se širina.

Puna kružnica (prečnik d, A = d²π/4)

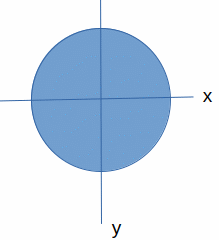
Moment inercije oko osa:

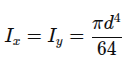
Polarni moment:

I_P = I_x + I_y = 2I_x

Koristi se kod zadataka uvijanja osovina.

Šuplja kružnica (cevast profil)

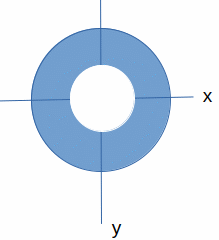
Aksijalni momenti inercije:

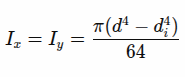
Polarni moment:

3.5. Trougao (osnovica b, visina h, A = b*h/2)

Oko osnove:

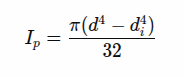
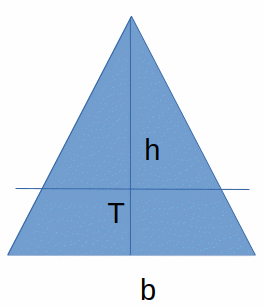
Oko težišne ose (paralelne osnovi):

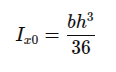
Oko y-ose (prolazi kroz vrh):

Stajnerova (paralelna) teorema – osnovni princip

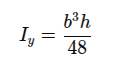
Ako je poznat moment inercije oko ose koja prolazi kroz centar preseka (težište),
onda je moment oko bilo koje paralelne ose:

I=I₀ + A * a²

gde je:

• I₀ – moment inercije oko centralne ose

• A – površina preseka

• a – rastojanje između osa

Momenti inercije složenih preseka (T, L, U, I profili)

Za složene preseke važi jednostavno pravilo:

1. Presek se razbije na osnovne oblike.

2. Za svaki se uzme:

   • površina A_i

   • moment oko sopstvene centralne ose I_0i

   • udaljenost njegovog centra od ukupne ose a_i

3. Primeni se Stajnerova teorema za svaki deo:

   I_i = I_0i + A_i * a_i²

4. Ukupni moment inercije:

   I=∑I_i