Osnovni pojmovi o istezanju i sabijanju (Hook-ov zakon)



Hookov zakon opisuje ponašanje materijala u oblasti elastičnih deformacija. Sila koja deluje duž ose predmeta teži da izduži ili sabije taj predmet – javlja se relativna deformacija kao odnos izduženja (skraćenja) i početne dužine ε = ΔL / L. Sila u materijalu izaziva napon σ = F / A pa možemo posmatrati dijagram napon – deformacija, sa koga se lepo vidi da je u pocetku naprezanja zavisnost linearna sve do granice proporcionalnosti P, zatim prelazi u blagu krivu do granice elqstičnosti E. Nakon te granice, deformacije postaju plastične (ireverzibilne) i nisu nam od interesa za ovaj predmet. Samo valja pomenuti granicu tečenja (gornju i donju), maksimalnu čvrstoću i granicu loma

Do granice proporcionalnosti Hookov zakon ima linearni oblik, a do graice elastičnosti deformacije su reverzibilne (materijal se vraća u prvobitno stanje. Taj deo se naziva oblast elastičnosti, i sve zadatke ćemo bazirati na izučavanju opterećenja u toj oblasti. Za zadatke nam prvo treba tabela gde su za različite materijale date vrednosti Jungovog modula elastičnosti E, kao i granice elastičnosti σE. Modul elastičnosti (E) je teoretska veličina i predstavlja naprezanje potrebno da se materijal izduži za 100% svoje prethodne dužine (dakle naprezanje kada je ε=1. To se u praksi obično ne dešava (materijal pukne pre toga). Granica elastičnosti σE je ‘opipljiva’ veličina i definiše maksimalno naprezanje nakon kojeg se materijal vraća u prvobitni položaj.





Materijal

Modul elastičnosti E [GPa]

Granica elastičnosti σE [MPa]

Čelik meki

210

200–250

Čelik tvrđi

210

300–400

Prohrom

200

200–300

Aluminijum

70

50–150

Bakar

110

60–150

Mesing

100

150–250

Liveno gvožđe

100–120

100–200

Poliamid (PA)

2–3

40–80

Drvo (duž vlakana)

8–15

40–100



Osim ove tabele, koristićemo i osnovne formule iz Hookovog zakona istezanja



1) Zatezna šipka od čelika

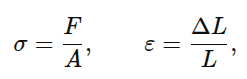
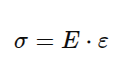
Okrugla šipka d=12mm, L=1,8m, opterećena silom F=20kN.
Traži se: σ, ΔL, ε.
Rešenje (brojčano): A=πd2/4=113,1mm2.
σ≈176,8MPa, ΔL≈1,52mm, ε≈0,000842.

2) Ravna letva od aluminijuma

Pravougaoni presek b×h=20×5mm⇒A=100mm2, L=0,75m, sila F=6kN.
Naći izduženje.
Rešenje: ΔL≈0,643mm (σ≈60MPa).

3) Dopušteno izduženje → najveća sila

Čelična zatezna veza d=10mm, L=0,50m. Dopušteno izduženje je ΔLmax​=0,25mm.
Kolika je najveća dozvoljena sila?
Rešenje: Fmax​≈8,25kN (pripadajuće σ≈105MPa).

4) Bakarna spona – zadato izduženje

Bakarna šipka d=8mm, L=250mm se izduži ΔL=0,40mm.
Odredi silu i napon.
Rešenje: F≈8,85kN, σ≈176MPa.

5) Dve paralelne šipke (deljenje opterećenja)

Viseći nosač drže dve jednako duge prohromske šipke (svaka d=6mm, L=0,40m). Ukupno opterećenje je 8kN (ravnomerno se deli).
Naći izduženje svake šipke i ukupno „sleganje“ sistema.
Rešenje: Svaka nosi 4kN. ΔL≈0,283mm po šipci, pa je i ukupno sleganje ≈0,283mm. σ≈141,5MPa.

6) Poliamidna traka (demonstracija velikog istezanja)

Poliamidna traka A=60mm2, L=1,2m, F=1,5kN.
Odredi ΔL.
Rešenje: ΔL≈12mm (σ≈25MPa).

7) Mesing – provera uslova izduženja

Letva od mesinga b×h=15×3mm⇒A=45mm2, L=0,30m, sila F=1,2kN.
Da li je ispunjen uslov ΔL≤0,15mm?
Rešenje: ΔL≈0,080mm → uslov ispunjen (σ≈26,7MPa).

8) Dimenzionisanje prečnika zbog ograničenog izduženja

Čelična veza dužine L=2,0m prenosi silu F=15kN. Traži se minimalni prečnik okrugle šipke ako je zahtev ΔL≤0,50mm.
Rešenje:
Potrebna površina A=EΔLFL​≈286mm2.
Minimalni prečnik d=π4A​​≈19,1mm.

9) Zadato istezanje (mereno) → sila preko σ=Eε

Čelična šipka d=14mm, L=500mm. Izmeren relativni pomak daje deformaciju ε=0,12%.
Naći silu.
Rešenje: σ=Eε≈252MPa ⇒ F=σA≈38,8kN.